DocAide Exemples aléatoires

Sommaire

Ce document détaille et complète la partie "Insertion d'exemples à données aléatoires" du DocAide Documents .
Il présente aussi des exemples de dessins dynamiques et d'insertion de figures GeoGebra.

Exemples aléatoires

Bases de la programmation des exemples aléatoires
Boucles et branchements
Formulaire d'entrée de variables
Formulaire outil
Créer un exemple à partir d'un exercice . Par exemple, cet exemple Nombre dérivé .
Exemples à solution cachée (avancé)
- Equation du second degré
- Proportionnalité et son code

Dessins dynamiques

Aide pour les figures
- Dessins et figures dynamiques
- Insertion à l'aide de jsxgraph d'une figure GeoGebra (sans Java)
Exemples de dessins
1. Interprétation des signes dans une équation de droite et son code
2. Interprétation graphique pour une équation du second degré et son code
3. Fractions de segment et son code
4. Placer un point sur une droite et son code

Bases de la programmation des exemples aléatoires

Pour les questions traitées ici, voyez aussi l'Aide 7 et 8 ou la partie "Insertion d'exemples à données aléatoires" dans DocAide Documents.

La définition des variables et l'aléatoire

Les variables utilisées dans les exemples sont les mêmes que celles des exercices : text, integer, rational, matrix..., seule la syntaxe de définition change. Pour la liste des paramètres aléatoires, consulter l' Aide de Createxo .

\def{text p=pomme} écrit pomme quand on écrit \p dans la page. Remarquez le \ devant le nom de la variable quand on l'utilise.
\def{text p=random(pomme, poire)} écrit aléatoirement pomme ou poire quand on écrit \p dans la page. Il suffit de recharger la page.
\def{integer n=4} définit un entier n, qu'on appelle avec la commande \n et qui vaut 4.
\def{integer n=random(1..4)} définit un entier n qu'on appelle avec la commande \n et qui vaut aléatoirement 1, 2, 3 ou 4.

On peut définir une liste et en récupérer les éléments :

\def{text liste = 1,2, x, 3/4}
\def{text s = item(3,\liste)}    ou    \def{text s = \liste[3]}

On peut définir toute sorte de matrice, les lignes sont écrites les unes en dessous des autres et les éléments sont séparés par une virgule, et en récupérer les éléments :
```
\def{matrix A = la fonction est positive, oui
la fonction est négative, non}
\def{text s = item(1,row(2,\A))}   ou   \def{text s = \A[2;1]}
```

Renouveler les données

Si on clique sur un lien Nouvel exemple défini par \reload{Nouvel exemple}, on donne de nouvelles valeurs aux paramètres aléatoires.
On obtient le même effet en cliquant sur le lien Recharger du bandeau.

Le double de 10 est 20.
Un kilogramme de cerises vaut 5 euros. Le prix des cerises est proportionnel à la masse de cerises et le coefficient de proportionnalité est 5.

Pour la suite, utilisez le lien Suiv. dans le bandeau ou une flèche latérale.

Boucles et branchements

Boucle

La boucle \for{i=1 to 10}{\i, } permet d'afficher les entiers de 1 à 10.

Compte de 5 en 5 de 5 à 15. Solution : 5, 10, 15

Dans la page Cacher la solution dans un exemple de la partie 5 (Insertion d'exemples à données aléatoires) du DocAide Documents, vous trouverez cet exemple avec sa solution cachée affichable à la demande, le code est donné.

Un branchement

Le code :

\def{ text mot = randitem( exercice, exercices) }
\if{\mot issametext exercice}{un}{des}\mot

donne

Voici des exercices .

Un autre branchement

Le code :

\def{ integer p = random(-1,+1)*random(1..10) }
\def{ text signe = \p>0? positif:négatif }
L'entier \n est strictement \signe.

donne

L'entier 10 est strictement positif.

Formulaire d'entrée de variables

On peut demander au lecteur d'entrer une valeur :

Le code :

\form{.}{expform}{
    Entrez votre expression : 
    <input size = 30 name = parm1 value = "\parm1">
    <input type = hidden value = OK>
    }
  \def{real N = \parm1}
   L'expression vaut \N.

donne

L'expression vaut 0.

ou plusieurs valeurs :

La somme des entiers 2 et 3 vaut 5.

Voir le code

\def{integer parm2=randint(0 .. 9)}
\def{integer parm3=randint(0 .. 9)}
 \form{.}{expform}{
    Entrez deux entiers :
    <input size = 10 name = parm2 value = "\parm2">
et
    <input size = 10 name = parm3 value = "\parm3">
    <input type = submit value = OK>
}
  \def{integer N = \parm3 + \parm2 : 0}
 La somme des entiers \(\parm2) et \(\parm3) vaut \(\N).

Formulaire outil

WIMS propose différents outils rapides qu'on peut insérer dans une page html donc dans un DocWims. En voici un exemple avec une question à données aléatoires.

Factorisation

Factorisez l'expression suivante et utilisez l'outil pour vérifier votre résultat.

Créer un exemple à partir d'un exercice

Vous pouvez transformer un exercice en exemple aléatoire à l'aide de quelques simples modifications. On peut ainsi récupérer des dessins intéressants. C'est un moyen pour présenter une solution rédigée d'un exercice proposé dans une feuille.

Commencez par importer le source de l'exercice dans votre classe et copiez-le dans un fichier text, par exemple gedit.
Les lignes qui ne commencent pas par \ sont des commentaires, vous pouvez les effacer ou les inclure dans un \comment{}.
L'énoncé est dans \statement. Vous supprimez la commande \statement{ ainsi que }.
Les commandes qui définissent les variables doivent être modifiées ainsi : \text{a=...} est remplacé par \def{text a=...}. On peut le faire automatiquement en utilisant rechercher et remplacer.

Nombre dérivé

Voici un exemple construit à partir du source de l' exercice .

Soit la fonction f définie sur

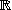, par f(x)= 2x²- 5x + 1. Voici les étapes pour calculer le nombre dérivé de f en x= -1.

Calculer f(-1) : f(-1)=
Exprimer f(-1+h) en fonction de h : f(-1+h)=
Exprimer le rapport en fonction de h:
Le nombre dérivé de f en x= -1 est la limite de quand h tend vers 0, c'est-à-dire .

Exemples à solution cachée

Si on veut cacher la solution et ne l'afficher qu'à la demande, il est impossible de la mettre dans un pli car à l'ouverture du pli, les données sont renouvelées. C'est pourquoi, on utilise la commande \link. La page Cacher la solution dans un exemple dans la partie 5 (Insertion d'exemples à données aléatoires) du DocAide Documents présente les détails de cette technique. On y trouve l' exemple de boucle avec sa solution cachée.

Résolution d'une équation du second degré

Cet exemple, comme souvent, n'est pas programmé comme on résout l'exercice. On se donne des racines aléatoires et on établit l'équation. Les paramètres à transmettre seront donc les racines et bien sûr le paramètre N qui décide du choix entre "donner la solution" ou "renouveler l'exemple".

Résoudre l'équation = 0.

Solution

Code de cet exemple.
On commence par définir le paramètre N qui décide du choix entre "donner la solution" ou "renouveler l'exemple" et le nom du lien pour recharger la page. Ce lien est placé après l'énoncé, c'est la dernière ligne du code.

\def{integer N = \parm1 = 1 ? 2 : 1}
\def{text lien=\N=1 ? Solution:Nouvelle équation}

Voici la mise en place des données de l'exemple.

Si N vaut 1, les données sont prises aléatoirement car on a renouvelé l'exemple.
Si N vaut 2, les données sont celles transmises par la commande (dernière ligne) qui renouvelle la page pour afficher la solution. Elles sont utilisées pour le calcul de la solution.

\def{integer e = \N=1 ? random(1..4):\parm2}
\def{integer f = \N=1 ? random(-2..5):\parm3}

Calcul nécessaire pour établir l'équation et la solution.

\def{integer b = -(\e + (\f))}
\def{integer c = \e*\f}
\def{integer d = (\b)^2-4*(\c)}
\def{text E = maxima(x^2+\b*x+\c)}

Affichage de l'énoncé.

Résoudre l'équation \(\E = 0).

Affichage de la solution quand N vaut 2. La solution dépend de la valeur du discriminant.

\if{\N=2}{Le discriminant vaut \(\d).}
\if{\d = 0 and \N=2}{L'équation a une seule solution : \(\alpha = \e).}
\if{\d <> 0 and \N=2}{L'équation a  deux solutions : \(\alpha = \e) et \(\beta = \f).}

Voici la commande qui transmet les paramètres et affiche le lien pour recharger la page.

\link{.}{\lien}{exemple}{parm1=\N&parm2=\e&parm3=\f}

Proportionnalité

Voici un exemple construit à partir du source de l' exercice "Tableau 1". Le code est décrit à la page suivante.

Complète le tableau de proportionnalité suivant :

3	9

Quel est le coefficient de proportionnalité ?

Réfléchis puis regarde la réponse

Code du tableau de proportionnalité

Pour renouveler la page

\def{integer N = \parm1= 1 ? 2 : 1}
\def{text lien=\N=1 ? Réfléchis puis regarde la réponse:Nouvelle question}

Source de l'exercice

\def{rational  prop=\N=1 ? random(randint(2..9), random(3/2,1/2,5/2)):\parm2}
\def{integer   a=\N=1 ? randint(3..6):\parm3}
\def{integer   b=\N=1 ? randint(4..9):\parm4}
\def{integer   b=\a=\b? \b+1}
\def{rational    aa=\a*\prop}
\def{rational    bb=\b*\prop}
\def{text  pr=\prop}
\def{text  choix=\N=1 ? random(1,2,3,4):\parm5}

Construction de la réponse

\def{text tableauReponse=<table align="center" border=1>
<tr align="center"><td width="50%">\a</td>
<td>\b</td></tr>
<tr align="center"><td>\aa</td>
<td>\bb</td>
</tr>
</table>
<br> Le coefficient de proportionnalité est  \pr.}

Définition de la variable reponse qui est vide si N vaut 1.

\def{text reponse=\N=2 ? La solution est \tableauReponse:}

Affichage de l'énoncé

Complète le tableau de proportionnalité suivant :
<table align="center" border=1>
<tr align="center"><td width="50%">
\if{\choix=1}{ }{\a}</td><td>\if{\choix=2}{ }{\b}</td></tr>
<tr align="center"><td>\if{\choix=3}{ }{\aa}</td><td>
\if{\choix=4}{ }{\bb}</td>
</tr>
</table><br>
Quel est le coefficient de proportionnalité ?

Affichage de la variable reponse et du lien pour renouveler l'exemple ou afficher la réponse.

\reponse
<br>
\link{.}{\lien}{}{parm1=\N&parm2=\prop&parm3=\a&parm4=\b&parm5=\choix}

Dessins et figures dynamiques

Pour les dessins dynamiques à l'aide de commandes WIMS, consultez

l'aide des DocWims (§7),
le paragraphe dessin dans le DocAide Exercices OEF,
l'aide de Createxo
le polycopié pdf "Introduction à la programmation" dans la classe d'exemple Autre / Développement de ressources.

Pour l'insertion de figures GeoGebra, téléverser la figure dans geogebratube, copier le code html fourni par la fonction "imbriquer" et le coller dans la page du DocWims concernée.

On peut aussi transformer des figures GeoGebra simples en jsxgraph. Voir page suivante.

Insertion à l'aide de jsxgraph d'une figure GeoGebra (sans Java)

La commande slib(geo2D/ggb2jsxgraph ... ) permet d'afficher une figure GeoGebra simple avec le logiciel jsxgraph qui n'utilise pas java à l'affichage.

Voici le code :

\def{text C=slib(geo2D/ggb2jsxgraph
blabla
,400x400,1)}

blabla est soit le nom du fichier ggb déposé dans Dépôt de fichier, soit la liste des caractères suivants value= dans la source de la figure exportée en html ,
400x400 la taille du cadre de la figure,
1 le numéro d'ordre de la figure dans la page.

Interprétation des signes dans une équation de droite

Quelle est l'équation de la droite représentée ci-contre ?

Réponse

Le code est à la page suivante.

Code du choix d'une droite

\def{integer P = \parm1 = 1 ? 2 : 1}
\def{text lien=\P=1 ? Réponse:Nouvelle droite}


\def{integer a=\P=1 ?randint(1..4):\parm2}
\def{integer b=\P=1 ?randint(1..6):\parm3}


\def{matrix M=\a*x + \b, positive, positif, croît, positif
- \a*x +\b, positive, positif, décroît, négatif
\a*x - \b, négative, négatif, croît, positif
- \a*x - \b, négative, négatif, décroît, négatif}


\def{integer r=rows(\M)}
\def{text liste=y = texmath(pari(\M[1;1]))}
\for{j=2 to \r}{
\def{text liste=\liste,y = texmath(pari(\M[\j;1]))}}
\def{integer n=\P=1?randint(1..\r):\parm4}
\def{function f=maxima(\M[\n;1])}


\def{text  dessin =
   xrange -7.2,7.2
   yrange -7.2,7.2
   hline 0,0,black
   arrow 0,0,1,0,8, black
   arrow 0,0,0,1,8, black
   text black,0.2,-0.2,medium,0
text black,6.8,-0.2,medium,x
text black,0.2,7,medium,y
   vline 0,0,black }
\def{text graphe=plot red, \f}


\def{text solution=
 Soit \(y=ax+b) une équation de la droite représentée.
 <ul><li>
Comme la droite rencontre l'axe des y en un point d'ordonnée \M[\n;2],
le nombre \(b) est  \M[\n;3].</li>
<li>
Comme sur la droite, \(y)  \M[\n;4] avec \(x),
le nombre \(a) est  \M[\n;5].</li></ul>
Une équation de la droite est donc \liste[\n].<br>}


\def{text solution=\P=2? \solution:}


<div class="flaot_right">
  \draw{ 200,200 }{
     \dessin
     \graphe} </div>


Quelle est l'équation de la droite représentée ci-contre ?
 <ul>
 <li>\liste[1]</li>
 <li>\liste[2]</li>
 <li>\liste[3]</li>
 <li>\liste[4]</li></ul> </td>
 <td width="50%">


\solution
\link{.}{\lien}{exemple}{parm1=\P&parm2=\a&parm3=\b&parm4=\n}

Interprétation graphique pour une équation du second degré

Voici la parabole d'équation y = :

Les points rouges ont pour abscisse les solutions 3 et -2 de l'équation = 0.
Le point vert est le sommet de la parabole. Ses coordonnées sont , soit dans notre exemple (0.5, -6.25).

Le code est à la page suivante.

Exercice : Allure d'une parabole

Code de la parabole

\def{integer e = random(1..4)}
\def{integer f = random(-2..5)}
\def{integer b = -(\e + (\f))}
\def{integer c = \e*\f}
\def{integer d = (\b)^2 - 4*(\c)}
\def{text E=maxima(x^2 + \b*x + \c)}
\def{real s1=-\b/2}
\def{real s2=-\d/4}

Voici la parabole d'équation \(y = \E) :

\draw{300,300}{xrange -10.2,10.2
   yrange -10.2,10.2
   parallel -10,-10,10,-10,0,1,21, grey
   parallel -10,-10,-10,10,1,0,21, grey
   hline 0,0,black
   arrow 0,0,1,0,8, black
   arrow 0,0,0,1,8, black
   vline 0,0,black
   plot blue , \E
fcircle \e,0,6,red
fcircle \f,0,6,red	
fcircle \s1,\s2,6,green}

Les points rouges ont pour abscisse les solutions \(\e) et \(\f) de l'équation \(\E = 0). 

Le point vert est le sommet de la parabole. Ses coordonnées 
sont \((-\frac{b}{2},-\frac{\Delta}{4})), soit dans notre exemple \((\s1, \s2)).

\reload{Autre dessin}

Fractions de segment

Le segment rouge a pour longueur de la longueur du segment [AB].
Le segment vert a pour longueur de la longueur du segment [AB].

Les fractions ont même dénominateur, la plus grande est celle dont le numérateur est le plus grand.
Code de cet exemple

\def{integer den=random(3,4,5,6,10,12,15,24,30)}
\def{integer num1=randint(1..\den-1)}
\def{integer num2=randint(1..\den-2)}
\def{integer num2=\num1=\num2?\num2 +1:\num2}
\def{integer espace=60/\den}
\def{rational f1=\num1*\espace}
\def{rational f2=\num2*\espace}
\def{text fraction1=texmath(\num1/\den)}
\def{text fraction2=texmath(\num2/\den)}
\def{text droite1=xrange -0.2,60.2
  yrange -1.5,3
linewidth 3
hline 0,0,black
parallel 0,-0.7,0,0.7,\espace,0,\den,blue
linewidth 6
  line 0,-1,0,1,black
  text black,0,2,medium,A
  line 60,-1,60,1,black
  text black,59,2,medium,B
  line 0,0.4,\f1,0.4,red
  line 0,-0.4,\f2,-0.4,green
 }

On pourrait illustrer de même le cas où les fractions ont même numérateur.

code de la comparaison de fractions

\def{integer den=random(3,4,5,6,10,12,15,24,30)}
\def{integer num1=randint(1..\den-1)}
\def{integer num2=randint(1..\den-2)}
\def{integer num2=\num1=\num2?\num2 +1:\num2}
\def{integer espace=60/\den}
\def{rational f1=\num1*\espace}
\def{rational f2=\num2*\espace}
\def{text fraction1=texmath(\num1/\den)}
\def{text fraction2=texmath(\num2/\den)}
\def{text droite1=xrange -0.2,60.2
  yrange -1.5,3
linewidth 3
hline 0,0,black
parallel 0,-0.7,0,0.7,\espace,0,\den,blue
linewidth 6
  line 0,-1,0,1,black
  text black,0,2,medium,A
  line 60,-1,60,1,black
  text black,59,2,medium,B
  line 0,0.4,\f1,0.4,red
  line 0,-0.4,\f2,-0.4,green
 }

Placer un point sur une droite

Voici un exemple construit à partir du source de l' exercice . Le code est à la page suivante.

Voici le barycentre G de { (A;),(B; - )} :

Placer un point sur une droite (code)

Code de l'exercice de la page précédente

Choix paramètre entier ou rationnel mais on ne veut pas c=1.

\def{integer choix=random(1,2)}
\def{integer b=random(1..5)}
\def{rational c=\choix=1?random(-1,-2,2):random(-1,-2,-3,2,3)/\b}
\def{rational c=\c=1?2}
\def{rational ca=1-\c}

Définitions pour l'énoncé :

\def{text s1=\c>0?+:-}
\def{rational mc=-1*(\c)}
\def{text tc=\c>0?\c:\mc}
\def{text tc=wims(replace internal / by , in \tc)}
\def{text tc=items(\tc)>1?\frac{\tc[1]}{\tc[2]}}
\def{text tca=\ca}
\def{text tca=wims(replace internal / by , in \tca)}
\def{text tca=items(\tca)>1?\frac{\tca[1]}{\tca[2]}}

Définitions pour le dessin :

\def{integer fx=\c*(\b)}
\def{integer fy=0}
\def{integer Ox=403}
\def{integer ex=31}
\def{integer \fxx=\Ox+\ex*\fx}
\def{integer \fxxm=\fxx-0.3*\ex}
\def{integer \fxxp=\fxx+0.3*\ex}
\def{text repimage=xrange -13,13
  yrange -1.5,3
  hline 0,0,red
  parallel -12,-0.2,-12,0.2,1,0,2,blue
  parallel -10,-0.4,-10,0.4,5,0,5,blue
  parallel -9,-0.2,-9,0.2,1,0,4,blue
  parallel -4,-0.2,-4,0.2,1,0,4,blue
  parallel 1,-0.2,1,0.2,1,0,4,blue
  parallel 6,-0.2,6,0.2,1,0,4,blue
  parallel 11,-0.2,11,0.2,1,0,2,blue
  text red,-0.1,1.5,medium,A
  text red,\b-0.1,1.5,medium,B
  text green,\fx-0.1,-0.5,medium,G
  line 0,-0.2,\a,0.2,red
  line \b,-0.2,\b,0.2,red
  line \fx,-0.2,\fx,0.2,red
  }

Enoncé :

Voici le barycentre \(G) de {\((A,\tca),(B, \s1 \tc))} :
<center>
\draw{800,64}{\repimage}
</center>
\reload{Nouveau barycentre}