OEF réduction d'endomorphismes
--- Introduction ---
Ce module regroupe pour l'instant 16 exercices sur la réduction
des endomorphismes et les classes de similitude (niveau L3).
La représentation en partitions est évoquée dans deux exercices
et sera développée plus tard (exercices en préparation).
Décomposition semi-simple de Jordan-Chevalley
Donner la partie semi-simple de la matrice
Il s'agit d'une matrice
dont le polynôme minimal n'a pas de facteurs multiples, commutant avec
et telle que
soit nilpotente. S =
On écrira la matrice ligne par ligne en séparant les coefficients par des virgules. Pour copier-coller dans des outils : .
Décomposition de Jordan-Chevalley
Une matrice A de Mn(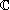 ) s'écrit comme la somme d'une matrice diagonalisable S et d'une matrice N nilpotente commutant entre elles : A = S + N (décomposition de Jordan-Chevalley (Dunford)). Pour A =
, calculer la matrice
On écrira la matrice ligne par ligne en séparant les coefficients par des virgules.
) s'écrit comme la somme d'une matrice diagonalisable S et d'une matrice N nilpotente commutant entre elles : A = S + N (décomposition de Jordan-Chevalley (Dunford)). Pour A =
, calculer la matrice
On écrira la matrice ligne par ligne en séparant les coefficients par des virgules. Pour copier-coller dans des outils : [].
Partitions et décomposition de Frobenius
Soit
un endomorphisme d'un espace vectoriel de dimension finie
. Les invariants de similitude sont
de degrés respectifs . Dessiner le diagramme de Young associé à l'endomorphisme
Pratique de Jordan
La matrice
suivante est nilpotente.
On désire calculer sa décomposition de Jordan en utilisant
.
Donner les dimensions des noyaux de
Calculer la taille des blocs de Jordan par ordre décroissant :
Choisir un vecteur
engendrant un sous-espace cyclique de polynôme minimal le polynôme minimal de
.
~ Choisir une forme linéaire
nulle sur les
pour
et non nulle sur
en la donnant par sa matrice ligne :
Vous avez choisi le vecteur
et la forme linéaire
.
Soit
le plus petit-espace vectoriel stable par la transposée de
contenant
. Donner des équations (indépendantes) du sous-espace de
orthogonal à
sous la forme B (x_1, ... x_)~= 0 B =
Vous avez donné comme équations de l'orthogonal de
 X = 0
Donner une base dans laquelle la matrice de
est la matrice de Jordan
(on écrira les vecteurs en colonne dans la base canonique.)
X = 0
Donner une base dans laquelle la matrice de
est la matrice de Jordan
(on écrira les vecteurs en colonne dans la base canonique.)
Matrice de Jordan et noyaux itérés
La matrice
suivante est telle que
est nilpotente.
Donner les dimensions des noyaux de
Jordan et invariants de similitude
La matrice
suivante est telle que
est nilpotente.
Donner les invariants de similitude de
en indiquant la liste des exposants de
des invariants.
Partitions et décomposition de Jordan
La matrice
suivante est telle que
est nilpotente. Dessiner le diagramme de Young associé à la matrice
Quelle est la dimension du noyau de
?
Nombre de classes de similitude I
Donner le nombre de
des matrices à coefficients dans 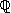 de polynôme caractéristique
de polynôme caractéristique
(décomposition de
en facteurs irréductibles)
Nombre de classes de similitude II
Donner le nombre de
des matrices à coefficients dans 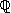 de polynôme caractéristique
de polynôme caractéristique
(décomposition de
en facteurs irréductibles) et de polynôme minimal
Nombre de classes de similitude III
On associe à une matrice sur un corps
la suite de ses invariants de similitudes
, ...,
vérifiant
Donner la longueur de la suite possible la plus longue
La longueur de la suite possible la plus longue est
(vous vous êtes trompé)
sachant que le polynôme caractéristique de la matrice est
(décomposition de
en facteurs irréductibles) et que le polynôme minimal est
.
L'exercice comporte deux étapes.
Donner un exemple d'une telle suite :
(
) 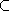 (
)
(
)
Matrices nilpotentes et tableaux de Young
Combien y a-t-il de classes de similitude de matrices carrées nilpotentes de taille telles que la dimension du noyau de
soit :
Vous avez répondu . Non, il
Il
y a
classe
classes
de similitude de matrices carrées nilpotentes de taille telles que la dimension du noyau de
soit .
Dessiner le tableau de Young associé en partant du carré bleu isolé :
Voici les tableaux de Young associés à de telles classes de similitude sauf un. Le dessiner en partant du carré bleu isolé :
Polynômes d'endomorphismes et projecteurs
Soit
un espace vectoriel de dimension finie et soit
un endomorphisme annulé par
avec
et
. Les deux polynômes
et
sont premiers entre eux. La projection de
sur
est un polynôme d'endomorphisme en
. Quel est ce polynôme (on en prendra un de degré minimal dans 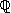 [x]).
[x]).
Pour copier-coller dans des outils : , .
Endomorphismes et projecteurs
Soit
un espace vectoriel de dimension finie muni d'une base et soit
l'endomorphisme donné par la matrice
. Soit
. Le polynôme minimal de
est
 avec
=
. Vérifier que
et
sont premiers entre eux et que
. Calculer la matrice de la projection de
sur
parallèlement à
On écrira la matrice ligne par ligne en séparant les coefficients par des virgules. Pour copier-coller dans des outils : .
avec
=
. Vérifier que
et
sont premiers entre eux et que
. Calculer la matrice de la projection de
sur
parallèlement à
On écrira la matrice ligne par ligne en séparant les coefficients par des virgules. Pour copier-coller dans des outils : .
Endomorphisme semisimple
Soit un endomorphisme
diagonalisable. Dans une certaine base, sa matrice est
Dessiner (dans la même base) une matrice commutant avec
en mettant les coefficients pouvant ne pas être nuls en bleu.
Carré d'un endomorphisme nilpotent
Soit
une matrice carrée nilpotente dont le diagramme de Young est le suivant Dessiner le diagramme de Young de
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur de web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
Description: collection d'exercices sur la réduction des endomorphismes. interactive exercises, online calculators and plotters, mathematical recreation and games
Keywords: interactive mathematics, interactive math, server side interactivity, mathematics, linear algebra, algebra, endomorphisme, réduction, jordan, chevalley, dunford
 (
)
(
)  ) s'écrit comme la somme d'une matrice diagonalisable S et d'une matrice N nilpotente commutant entre elles : A = S + N (décomposition de Jordan-Chevalley (Dunford)). Pour A =
, calculer la matrice
On écrira la matrice ligne par ligne en séparant les coefficients par des virgules.
) s'écrit comme la somme d'une matrice diagonalisable S et d'une matrice N nilpotente commutant entre elles : A = S + N (décomposition de Jordan-Chevalley (Dunford)). Pour A =
, calculer la matrice
On écrira la matrice ligne par ligne en séparant les coefficients par des virgules.  X = 0
Donner une base dans laquelle la matrice de
est la matrice de Jordan
(on écrira les vecteurs en colonne dans la base canonique.)
X = 0
Donner une base dans laquelle la matrice de
est la matrice de Jordan
(on écrira les vecteurs en colonne dans la base canonique.) 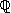 de polynôme caractéristique
de polynôme caractéristique
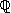 de polynôme caractéristique
de polynôme caractéristique
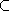 (
)
(
) 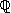 [x]).
[x]).  avec
=
. Vérifier que
et
sont premiers entre eux et que
. Calculer la matrice de la projection de
sur
parallèlement à
avec
=
. Vérifier que
et
sont premiers entre eux et que
. Calculer la matrice de la projection de
sur
parallèlement à