Isométries de l'espace
Sommaire
Ce document présente les isométries de l'espace affine euclidien orienté de dimension 3, noté E. L'espace vectoriel euclidien associé est noté .
Vous pouvez consulter ce document page à page ou à partir du tableau des isométries.
Il a pour base la partie VI du polycopié "Géométrie euclidenne" rédigé par Marie-Claude DAVID, Daniel PERRIN, Frédéric HAGLUND et utilisé à la préparation au CAPES de mathématiques à Orsay (Université Paris-Sud).
Les isométries vectorielles
Orientation d'un plan vectoriel de l'espace par un vecteur normalDroites propres et plans stables par une isométrie vectorielle
Les symétries orthogonales de l'espace vectoriel de dimension 3 (isométries vectorielles admettant trois valeurs propres réelles)
Les isométries vectorielles admettant une seule valeur réelle
Liste des isométries vectorielles (définitions)
Forme de la matrice d'une isométrie vectorielle dans une base orthonormée bien choisie
Nature d'une isométrie vectorielle donnée par sa matrice
dans une base othonormée directe
Orientation d'un plan vectoriel de l'espace par un vecteur normal
Soit un plan vectoriel de et soit un vecteur unitaire orthogonal à . Par définition, l'orientation de définie par est la suivante : si est une base orthonormée de , on dit que est directe si la base est directe.Remarque : Attention, si l'on change en , l'orientation de est renversée.
Droites propres et plans stables par une isométrie vectorielle
Comme est de dimension 3, tout endomorphisme de admet une ou trois valeurs propres réelles (comptées avec leur multiplicité)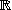 .
.
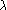 , soit
une droite propre associée à
, soit
une droite propre associée à
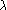 et soit
le plan
orthogonal
à
. Alors, on a
et soit
le plan
orthogonal
à
. Alors, on a 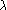 =
= 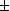 1 et le plan
est stable par
f.
1 et le plan
est stable par
f.
Démonstration : Les valeurs propres d'une isométrie sont 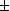 1
1
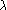 , on a
, on a
Les symétries orthogonales de l'espace vectoriel de dimension 3
La proposition suivante permet d'affirmer qu'une isométrie vectorielle qui admet trois valeurs propres réelles (comptées avec leur ordre de multiplicité) est diagonalisable, et plus précisément une symétrie orthogonale (bien sûr).
Démonstration : Soit
une droite propre de
pour la valeur propre 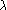 =
= 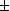 1 .
Comme le plan
est
stable par
, la restriction
est une isométrie
de
qui admet deux
valeurs propres réelles. Vue la classification des isométries en
dimension 2,
est donc l'identité, la symétrie centrale ou une symétrie
axiale. Dans tous les
cas,
est diagonalisable et donc
aussi. Comme les valeurs propres de
sont
1 .
Comme le plan
est
stable par
, la restriction
est une isométrie
de
qui admet deux
valeurs propres réelles. Vue la classification des isométries en
dimension 2,
est donc l'identité, la symétrie centrale ou une symétrie
axiale. Dans tous les
cas,
est diagonalisable et donc
aussi. Comme les valeurs propres de
sont 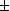 1,
il en résulte que
est une
symétrie.
1,
il en résulte que
est une
symétrie.
Liste des symétries orthogonales
Soit la symétrie orthogonale par rapport au sous-espace de . Il y a quatre cas :
- si , est l'identité (isométrie positive),
- si , est la réflexion de plan (isométrie négative),
-
si
,
est le demi-tour d'axe
(isométrie positive),
- si , est la symétrie centrale (isométrie négative).
Les isométries vectorielles admettant une seule valeur réelle
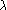 , soit
la droite propre
associée à
, soit
la droite propre
associée à 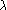 et
le plan
orthogonal à
.
et
le plan
orthogonal à
.
- La restriction de à est une rotation de .
-
Si on a
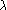 = 1 (resp.
= 1 (resp. 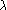 = -1) l'isométrie
est
positive (resp. négative).
= -1) l'isométrie
est
positive (resp. négative). -
Si est un vecteur unitaire de , il existe un unique réel
 modulo 2
modulo 2 tel que la matrice de
dans toute base orthonormée
directe de premier vecteur
soit
tel que la matrice de
dans toute base orthonormée
directe de premier vecteur
soit
Démonstration : Comme n'a pas de valeur propre réelle, la classification des isométries planes montre que c'est une rotation. Cela prouve les points 1 et 2.
On considère
l'orientation de
définie par
. Si
est une base directe de
,
est alors une base directe de
et si  est l'angle de la rotation
dans
muni de cette
orientation
, on
a bien la matrice annoncée dans
est l'angle de la rotation
dans
muni de cette
orientation
, on
a bien la matrice annoncée dans 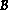 .
.
Liste des isométries vectorielles
Les symétries orthogonales
Soit la symétrie orthogonale par rapport au sous-espace de . Il y a quatre cas :- si , est l'identité (isométrie positive),
- si , est la réflexion de plan (isométrie négative),
-
si
,
est le demi-tour d'axe
(isométrie positive),
- si , est la symétrie centrale (isométrie négative).
Les rotations
Soit une isométrie vectorielle admettant une matrice du type
On dit que
est la rotation
vectorielle d'axe orienté
et d'angle

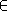
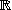 /2
/2
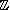 et on la note
.
et on la note
.
Une rotation est une isométrie positive.
- On notera que toutes les isométries vectorielles positives sont des rotations. Les demi-tours sont des rotations d'angle
 . En particulier elles admettent 1 comme valeur propre.
. En particulier elles admettent 1 comme valeur propre. - Attention, si on change l'orientation de , l'angle de la rotation est changé en son opposé:
. Cependant, l'angle de l'identité qui est nul et celui des demi-tours qui vaut ne changent pas si l'on change l'orientation de l'axe.
ne changent pas si l'on change l'orientation de l'axe.
Les antirotations
Soit une isométrie vectorielle admettant une matrice du type
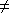 0,
0,  (mod 2
(mod 2 ).
).
On dit que
est l'antirotation vectorielle d'axe
et
d'angle
 .
.
Une antirotation est une isométrie négative.
Cette appellation nous semble commode, mais elle n'est pas standard. La plupart des auteurs ne donnent pas de nom spécifique à cette transformation.
Forme de la matrice d'une isométrie vectorielle dans une base orthonormée bien choisie
Toutes les isométries vectorielles admettent une matrice de la formeEn effet, on retrouve
- l'identité avec
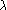 = 1 et
= 1 et  = 0,
= 0, -
les réflexions avec
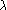 = -1 et
= -1 et  = 0,
= 0,
-
les demi-tours avec
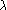 = 1 et
= 1 et  =
= 
- la symétrie centrale avec
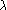 = -1 et
= -1 et  =
= 
et bien sûr
- les rotations avec
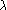 = 1 et
= 1 et  (mod 2
(mod 2 ) .
) .
- les antirotations avec
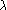 = -1 et
= -1 et  ,
,  (mod 2
(mod 2 ).
).
On notera que, sauf dans le cas des
symétries orthogonales, la droite engendrée par
est bien déterminée : c'est la droite propre
relative à 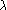 .
.
Remarques :
- La matrice d'une symétrie orthogonale est symétrique dans toute base orthonormée.
En effet, si A est la matrice d'une symétrie orthogonale dans une base orthonormée, elle vérifie et comme elle est orthogonale, elle vérifie aussi , dans A est symétrique.
- Dans la pratique, il n'est pas nécessaire de trouver la base où la matrice de est de cette forme pour déterminer sa nature (Voir la suite) .
Nature d'une isométrie vectorielle donnée par sa matrice
dans une base othonormée directe
Soit
B une base orthonormée directe de
et
une isométrie de
de matrice
A dans
B.
- La matrice A est orthogonale.
- L'isométrie
est une symétrie si et seulement si
A est une matrice symétrique.
En effet, si A est la matrice d'une symétrie orthogonale dans une base orthonormée, elle vérifie et comme elle est orthogonale, elle vérifie aussi , dans A est symétrique.
Dans ce cas :
- Si
n'est pas une symétrie,
admet la valeur propre
1 si elle est positive (c'est une rotation),
-1 si elle est négative (c'est une antirotation).
On oriente l'axe de
en choisissant un vecteur propre unitaire
relatif à la valeur propre
. L'angle
 est alors entièrement déterminé par les remarques suivantes :
est alors entièrement déterminé par les remarques suivantes :
- on a
- le signe de est le signe de où est un vecteur quelconque non colinéaire à .
Exercice 2
: Reconnaître un demi-tour, une réflexion, une rotation, une antirotation sur sa matrice.
Exercice 3
: Etude d'une rotation donnée par sa matrice.
Exercice 4
: Déterminer les éléments caractéristiques d'une rotation ou d'une antirotation.
Les isométries affines
Résultats importants de géométrie affineLes antidéplacements de l'espace
Droites et plans stables par une isométrie affine
Résultats importants de géométrie affine
Valeur propre 1 et points fixes
Commutation avec une translation
Décomposition des applications affines
- g est une application affine admettant un point fixe,
- le vecteur appartient à
- g et commutent.
D'après la proposition précédente, les affirmations (2) et (3) du théorème sont équivalentes.
Cas particulier des isométries affines
Les déplacements de l'espace
- l'identité,
- les translations de vecteur non nul,
- les rotations d'angle non nul
- les vissages avec et ,
Démonstration : Soit
f un déplacement et
l'application linéaire
associée. En vertu de la
liste des isométries vectorielles
,
est une rotation vectorielle d'angle
. Si
 est nul,
est l'identité, donc
f est une translation ou
l'identité.
Sinon, comme
admet la valeur propre 1, il y a deux cas :
est nul,
est l'identité, donc
f est une translation ou
l'identité.
Sinon, comme
admet la valeur propre 1, il y a deux cas :
- L'application f a un point fixe : dans ce cas elle a toute une droite de points fixes et c'est une rotation ,
- L'application f n'a pas de point fixe : dans ce cas, elle s'écrit comme composée d'une rotation et d'une translation de vecteur non nul (appartenant à la direction de l'axe de la rotation) qui commutent d'après le théorème de décomposition . C'est alors un vissage .
Définition d'une rotation affine
Soit D une droite, orientée par le choix d'un vecteur non nul de , et soit .On appelle rotation d'axe
orienté
et d'angle
 l'application affine notée
définie par :
l'application affine notée
définie par :
- pour tout point a de D,
-
est la rotation vectorielle
d'axe
et d'angle
 .
.
- Comme laisse fixe tous les vecteurs de , il suffit d'imposer la relation pour un point .
- La rotation laisse stable tout plan perpendiculaire à son axe et agit dans un tel plan comme une rotation plane de centre le point fixe de la rotation dans ce plan (intersection de l'axe et du plan). Faites un dessin !
- les symétries centrales où a est un point de E,
-
les antirotations
de
centre
a, d'axe
D et d'angle
 ,
,
- les réflexions orthogonales où H est un plan
- les réflexions (orthogonales) glissées où H est un plan et où l'on a , .
-
est l' antirotation vectorielle d'axe et d'angle
 .
.
Les antidéplacements de l'espace
Démonstration : Les antirotations vectorielles n'ayant pas la valeur propre 1, les applications affines associées ont un unique point fixe et sont donc des antirotations affines .
En revanche, les réflexions ont la valeur propre 1 d'où les deux cas ci-dessus (voir Résultats importants de géométrie affine ).
Définition d'une antirotation affine
Soit D une droite de E que nous orienterons en choisissant un vecteur non nul de , soit a un point de D et soit , .On appelle
antirotation de centre
a, d'axe
et d'angle
 l'application affine
définie par :
l'application affine
définie par :
Une antirotation est la composée commutative d'une réflexion et d'une rotation.
Tableau des isométries de l'espace
Soit f une isométrie affine dont l'application linéaire associée est . On note A la matrice de dans une base orthonormée directe donnée de l'espace orienté. (Dans la pratique, il n'est pas nécessaire de calculer les valeurs propres de A pour connaître la nature de . Pourquoi ? )
ISOMETRIES POSITIVES |
ISOMETRIES NEGATIVES |
|||||
| 1 est valeur propre simple. Le choix d'un vecteur directeur de oriente le plan . et sont stables par . |
1 est valeur propre triple | 1 est valeur propre double. | 1 n'est pas valeur propre. | |||
|
a une valeur propre réelle. A n'est pas symétrique |
a
3 valeurs propres réelles
: 1,-1,-1 A est symétrique |
a 3 val. propres réelles : 1,1,-1 A est symétrique |
-1 est valeur propre triple |
-1 est valeur propre simple.
est une rotation d'angle
|
||
est une rotation d'angle
 distinct de
0 et distinct de
0 et
 . . |
|
|||||
,
rotation vectorielle
d'axe
orienté par
et d'angle
 distinct de
0 et distinct de
0 et
 . . |
est le demi-tour d'axe ou symétrie par rapport à | est la réflexion vectorielle par rapport à |
,
l'
antirotation vectorielle
d'axe
orienté par
et d'angle
 distinct de
0 et distinct de
0 et
 |
|||
| f a au moins un point fixe | Les points fixes de f forment une droite D de direction . Les plans perpendiculaires à D sont stables par f. | Tous les points sont fixes.
f est l'identité. |
f a un plan P de points fixes de direction . | f a un unique point fixe c. | ||
f est la
rotation affine
d'axe
D orienté
par
et d'angle
 distinct de
0 et de distinct de
0 et de
 . . |
f est le demi-tour (ou la symétrie) d'axe D. | f est la réflexion par rapport à P | f est la symétrie centrale de centre c. |
f est l'
antirotation affine
de centre
c, d'axe
orienté par
et d'angle
 distinct de
0 et distinct de
0 et
 où P est le plan passant par c orthogonal à D |
||
| f n'a aucun point fixe | f est un vissage . Sa décomposition canonique est : |
f est une translation de vecteur non nul. | f est une réflexion glissée . où est un vecteur non nul de . |
Comme n'admet pas la valeur propre 1, f a un unique point fixe. |
||