Commençons par des exemples
arithmétiques ou
numériques :
relatifs, réels ou rationnels :
I-2-1-1 Les nombres
Soit
l'ensemble des nombres relatifs ou
l'ensemble des nombres rationnels
ou
l'ensemble des nombres réels. Pour tous éléments
x,
y,
z de
K
-
;
-
(x + y) + z = x + (y + z) ;
-
0 + x = x + 0 = x ;
- il existe un élément
tel que
x + x' = x' + x = 0.
I-2-1-2 Les racines de l'unité
Soit n un entier
. Soit
l'ensemble des nombres complexes
pour
. C'est aussi l'ensemble des nombres complexes
z vérifiant
zn = 1.
Il vérifie pour
z dans
et
k et
j enties
-
;
-
;
-
;
-
.
Autrement dit, pour tous éléments
z,
z',
z'' de
-
;
-
;
-
;
- il existe un élément
tel que
.
Exercice
Dessiner
,
,
,
... Pour
,
prendre
et repérer successivement les produits
pour
:
z = z0,
z = z1,
z = z2, ...
n = 2
Exercice
Racines de l'unité et puissances
Sous-groupe de racines de l'unité
Sous-groupe de racines de l'unité II
Sous-groupe de racines de l'unité III
Des manipulations sur trois boules permettent aussi de trouver un groupe :
I-2-1-3 Permutations
(Lire la BD de Stewart : Ah les beaux
groupes - les chroniques de Rose Polymath (Belin) )
On a trois boules alignées. On peut ne pas changer leur ordre. C'est l'opération
identité
S0. On peut changer leur ordre en échangant les deux premières
(opération
S1 ), en faisant tourner les trois dernières (opération
S2) et en effectuant
ces opérations successivement. Donner
le résultat comme un tableau : si une opération nouvelle apparaît, lui donner un nom (
S3, ...) et la
rajouter.
|
S0 |
S1 |
S2 |
S3 |
S4 |
S5 |
S6 | ... | |
|
S0 | | | | | | | | | |
|
S1 | | | | | | | | | |
|
S2 | | | | | | | | | |
|
S3 | | | | | | | | | |
|
S4 | | | | | | | | | |
|
S5 | | | | | | | | | |
|
S6 | | | | | | | | | |
|
... | | | | | | | | | |
|
| | | | | | | | | |
On appelle ces opérations des
permutations
de l'ensemble des trois boules.
On note
la permutation qui transforme 1, 2, 3 en
a,
b,
c. Par exemple,
est la permutation qui transforme 1, 2, 3 en 2, 3, 1.
Exercice
Permutations I
Permutations II
Permutations III
Enfin, voici un exemple de groupe formé d'applications.
I-2-1-4 Applications
Soient les applications suivantes définies sur
:
On peut composer ces applications ; donner le résultat comme un tableau :
si une application
nouvelle apparaît, lui donner un nom et la rajouter.
|
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7
|
|
f1 | | | | | | |
|
|
f2 | | | | | | |
|
|
f3 | | | | | | |
|
|
f4 | | | | | | |
|
|
f5 | | | | | | |
|
|
f6 | | | | | | |
|
|
f7 | | | | | | |
|
Pouvez-vous vous arrêter ?

 entre 0 et
). On pose
.
entre 0 et
). On pose
.
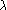 :
:
 tels que
et tels que
.
tels que
et tels que
.
 si
v = (a, 0).
si
v = (a, 0).
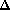 d'équation
X-2Y+5= 0 dans le repère
.
d'équation
X-2Y+5= 0 dans le repère
.