OEF edp --- Introduction ---

Ce module regroupe pour l'instant 3 exercices sur quelques équations aux dérivées partielles.

EDP et série de Fourier

Soit [0 , ]. On considère l'équation aux dérivées partielles

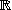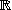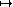où est une fonction de times RR dans RR : mapsto .

On développe la solution cherchée en série de Fourier par rapport à Quelle est l'équation différentielle vérifiée par les fonctions et (on l'écrira en utilisant pour la fonction, par exemple, ) ?

Quelle est la solution générale de cette équation qui vaut 1 en 0 ?

Ainsi,

avec et des réels.

On suppose que la condition initiale est . Exprimer et comme des intégrales :

EDP : équation de la chaleur

On veut déterminer la distribution des températures d'une tige homogène de longueur (ainsi, l'abscisse d'un point de la tige est comprise entre 0 et ). Les conditions imposées aux extrémités sont pour

On admet que vérifie l'équation aux dérivées partielles
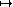On prolonge la solution mapsto en une fonction sur l'intervalle [ , ] puis par périodicité. Enfin, on développe la solution cherchée en série de Fourier par rapport à

Quelle est l'équation différentielle vérifiée par les fonctions (on l'écrira en utilisant pour la fonction, par exemple, ) ?

Quelle est la solution générale de cette équation qui vaut 1 en 0 ?

Ainsi, pour compris entre 0 et ,
avec des réels.

Soit la fonction définie par pour . On suppose qu'en , on a . Que peut-on dire de l'ordre des Calculer et .

EDP : équation des ondes

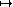Soit mapsto la fonction décrivant le mouvement d'une corde vibrante de longueur fixée aux extrémités (ainsi, l'abscisse d'un point de la corde est comprise entre 0 et ) :

U(0 , t) = U( , t) = 0

On suppose qu'au temps ,

où est la fonction définie par entre 0 et . On admet que vérifie l'équation aux dérivées partielles

En prolongeant la solution 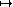mapsto en une fonction impaire sur l'intervalle [- , ], puis par périodicité et en développant la solution cherchée en série de Fourier par rapport à , on obtient une expression de la forme

Quelle est l'équation différentielle vérifiée par les fonctions (on l'écrira en utilisant pour la fonction, par exemple, ) ?

Si

,

la fonction vérifie l'équation différentielle du second ordre :

Ainsi, pour compris entre 0 et ,

avec des réels. Si sont les coefficients de Fourier de dans le développement en sinus, on a

Calculer , et . The most recent version

Cette page n'est pas dans son apparence habituelle parce que WIMS n'a pas pu reconnaître votre navigateur de web.

Pour accéder aux services de WIMS, vous avez besoin d'un navigateur qui connait les formes. Afin de tester le navigateur que vous utilisez, veuillez taper le mot wims ici : puis appuyez sur ``Entrer''.

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.

Description: collection d'exercices sur quelques équations aux dérivées partielles. interactive exercises, online calculators and plotters, mathematical recreation and games

Keywords: interactive mathematics, interactive math, server side interactivity, analysis, onde, dérivée partielle, fourier